NPR and NCR are the mathematical notation of two important concepts in mathematics, referred to as permutations and combinations. Both these concepts are similar in terms of what they mean to achieve, yet they are also different on a number of grounds.
Permutation – what are they?
A permutation is referred to as a mathematical calculation that describes a number of ways in which a set can be arranged. In the setting of these particular objects, the order of arrangement matters, and therefore, it is calculated as such.
Permutation is defined as NPR, and the formula for permutation is as follows:
N (p,r) = n! / (n-r)!
Where:
N = total number of items in the set
R = items taken for the permutation
! = Factorial
Usage of Permutations in Finance and Business
As mentioned earlier, it can be seen that permutations are used in order to describe the number of ways in which a set can be arranged. The usage of permutation in the business-related scenario is depicted in the following illustration:
Feliz Inc. seeks to build a warehouse network across the country. In order to execute this particular strategy, they have selected 10 locations, out of which they will eventually select 6. They will select 1 location, and then move on to the other location. In other words, they will be built sequentially.
In the example above, let’s assume the manager wants to find out the number of options that they have pertaining to selecting the possible location of these warehouses. In order to calculate these permutations, the following formula is used:
P (10,6) = 10! / (10-6)! = 10! / 4! = 151200
This means that there are 151200 possible permutations that are possible from the selected warehouses available to Feliz Inc. to choose from when it comes to these warehouses.
Alternatively, the concept of permutations can also be applied to portfolio managers. This is illustrated in the following example:
Let’s assume that there is a portfolio manager, that has shortlisted 10 companies to invest in a new fund which is supposed to constitute 2 companies. These companies are supposed to be shortlisted keeping in mind the fact that their weightage is not supposed to be equal, and hence, ordering is important in this case.
In order to calculate the number of ways in which the fund can be arranged, the following formula is used:
P (10, 2) = 10! / (10 – 2)! = 90
This means that the portfolio manager has around 90 possible permutations to arrange his funds from.
Combinations – What are they?
Combinations can be defined as the grouping of outcomes in which order is not really important. Unlike permutations where the order of the arrangement tends to be important, it can be seen that in the case of combinations, that does not necessarily hold true.
This mainly identifies the number of possible combinations that are possible as a result of objects being accumulated. Combinations are identified using the following notation:
NCR = N (c,r) = n! / r!(n-r)!
Where N = total number of items in the set
R = items taken for the permutation
! = Factorial
Usage of Combination – How it is used?
Combinations are widely used across numerous different types of business decisions that need to be taken place. The usage of combination is explained using the following illustration:
Let’s assume that Broman Co. is currently running a hedge fund, which is likely to include stock of rapidly growing companies. In this regard, it can be seen that there are around 20 companies that suit the set criteria. Out of these 20 stocks, 10 stocks need to be finalized to be included in the hedge fund.
In the example above, given the fact that the order in which the stocks are chosen does not matter, it is important to consider the fact that choosing these stocks at random would not really impact the final choices made in this regard.
Therefore, in order to calculate the possibilities from the pool of 20 selected stocks, the following calculation can be made:
C (20, 5) = 20! / 5! (20 -5)! = 15,504
This implies that there are around 15,504 ways in which these 20 stocks can be arranged in the form of groups of 5.
Differences between Permutations and Combinations
There is a notable difference between the calculation of permutation and combination. It is given as below:
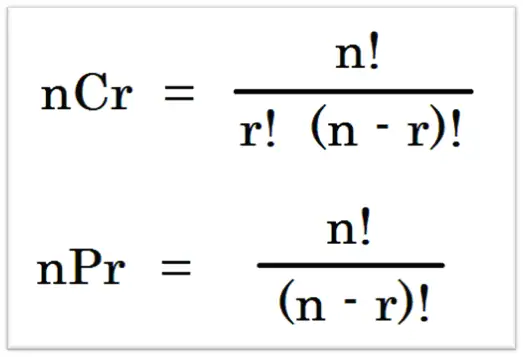
Differences between Permutations and Combinations can be summarized in the following table:
| Permutations | Combinations |
| nPr is the formula to find permutations of n objects taking r at a time. | nCr is the formula to find the unique permutations, otherwise known as combinations, of n objects taking r at a time. |
| Permutations address the question of how many possible groups of r objects from a set of n objects. | Combinations address the question of how many unique possible groups of r objects can be made from n objects. |
| It majorly concerns with the ‘arrangement’ of objects. | It is more about the ‘selection’ of objects. |
| Order matters in permutations. | An order does not matter in combinations. |
| Generally, NPR is greater than NCR. | Generally, NCR is lesser than NPR. |
Therefore, it can be seen that regardless of the fact that permutations and combinations involve mathematical numbers and equations, yet the major difference between NPR and NCR tends to be the relative importance of the order of arrangement. This main difference is further illustrated in the example given below:
Example of Permutation
How many 3 letter words can be formed from a given 5 letter word, given all the words can only be used once.
Since there are 5 options, it is important to calculate permutations, and since repetition is not allowed, the following formula is used:
P (n, r) = P (5, 3) = 5! / (2!) = 60
Therefore, this implies that there are around 60 3 letter words that can be formed from a given 5 letter word.
Example of Combinations
Out of 7 stocks, the company needs to choose any 3. What is the possible group of actions that can be formed in this regard?
In order to assess the possible number of combinations that are possible, it is important to consider the fact that weightage is considered to be equal for all the stocks that would be included in the analysis. Hence, the following combinations would be possible. They are as follows:
C (7, 3) = 7! / 3! (4!) = 35
