Introduction
Capital budgeting techniques are considered to be an important source of information, predominantly because of the fact that there are numerous different factors that come into play when it comes to considering projects involving considerable investment.
In this regard, it is considered important from the perspective of the accountants to ensure that these techniques are in place so that they can help the company to make viable decisions when they need to choose between two different projects.
Crossover Rate is considered to one very important metric in capital budgeting that helps companies to assess a combined outcome of two projects when analyzed together. The crossover rate is used to compare two different projects and is considered to be the same when used for two projects. Therefore, at certain times, it is also referred to as the Internal Rate of Return (IRR).
Definition
Crossover rate is referred to as the rate of return at which the net present values of two projects are equal. It is representative of the rate of return at which the net present value of one profile intersects with the net present value of another project.
Therefore, it can be referred to as the point where both projects have the same present value. It implies that the organization would be indifferent towards both these projects, in terms of one another.
Crossover rate is mostly used in capital budgeting related exercises. It is used to show when one investment project supersedes another because of the change in cost of capital (alternatively, the rate of return).
Therefore, to summarize the points mentioned above, it can be seen that cross over rate is defined as the cost of capital of two projects, which have equal Net Present Values. It involves two main variables, which are initial investments, as well as cash flows. It is mostly expressed as a percentage. It makes it easier for companies to choose between two different projects.
Formula
In order to calculate the crossover rate, the following example is used:
Net Present Value = [Cash Flow (Year 1) / (1+r)^ 1 ] + [Cash Flow (Year n) / (1 + r) ^n] – Ao, where,
Cash Flow year 1 = Cash Flow generated in the 1st year
Cash Flow year n = Cash Flow generated in the nth year
Ao = Initial investment in the project
The main premise here is to discount all the cash flows, in all the subsequent years over the life of the project, and then subtracting the initial investment from it. This means that if the life of one project is for 5 years, all the 5 cash flows are going to be included in the NPV calculation. Subsequently, the initial investment is not going to be discounted since it takes place in time zero (the current time). Therefore, the present value of the initial investment will not need to be discounted.
Crossover Rate: Understanding and Implications
As mentioned earlier, it can be seen that the crossover rate is the rate at which both the NPVs of the projects are equal. This implies that they have the same rate of return. This can be depicted in the following diagram:
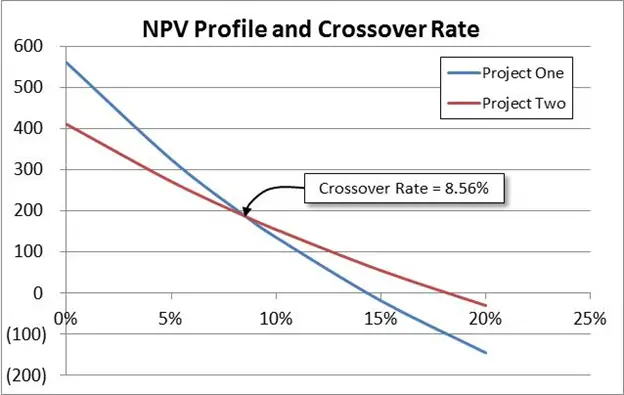
In the diagram above, it can be seen that both the NPVs have been plotted on a graph. Individually, Project One has a rate of return of 14.5% whereas for Project 2, the Rate of Return is around 18%. However, they both have a crossover rate at 8.56%, which is depicted by the intersection of both the lines in the diagram above.
Example
In order to understand how crossover rate works, the following example is used:
Capitol Co. is faced with 2 investment projects for which they need to choose and decide the way forward. The details of these projects are described below:
- Project A: Project A has a cost of $100,000. It is expected to render a cash flow of $20,000 in the first year, $120,000 in the second year and $300,000 in the third year.
- Project B: Project B has a cost of $50,000. It is expected to generate a cash flow of $150,000 in the first year, and $200,000 in the second year.
In order to calculate the crossover rate for both these projects, we need to calculate the rate of return at which both projects would be equal. This is calculated by equating NPVs.
NPV (Project A) = PV of Cash Flow 1, and Cash Flow 2 – Initial Investment
PV of Year 1 = $20,000 / (1+r) ^1 = 20,000 / (1+r)
PV of Year 2 = $120,000 / (1+r) ^2
Initial Investment = 100,000
Therefore, NPV (Project A) = [20,000 / (1+r)] + [$120,000 / (1+r) ^2] – $100,000
In the same manner, NPV for Project B will be calculated as follows:
NPV (Project B) = PV of Cash Flow 1, and Cash Flow 2 – Initial Investment
PV of Year 1 = $150000 / (1+r) ^1 = 20,000 / (1+r)
PV of Year 2 = $200,000 / (1+r) ^2
Initial Investment = $50,000
Therefore, NPV (Project B) = [150,000 / (1+r)] + [$200,000 / (1+r) ^2] + – $50,000
In order to calculate the crossover rate, both NPVs need to be combined. Hence:
NPV (project A) = NPV (project B)
[20,000 / (1+r)] + [$120,000 / (1+r) ^2] – $100,000 = [150,000 / (1+r)] + [$200,000 / (1+r) ^2] + – $50,000
Solving for r (the required rate of return) for both the projects:
r = 4.2%
This implies that at 4.2%, both the projects will have the same NPV.
Alternative Method of Calculating Crossover Rate
Crossover rate can also be alternatively calculated using the following steps:
- Determination of the cash flow of both the projects involved
- Finding the difference of initial investment in both the projects
- Finding the difference in cash flow for all the subsequent periods.
- Developing an IRR equation by equating the NPV equation with 0.
- Solving the equation for r, to arrive at the crossover rate.
This particular method is somewhat similar as the method prescribed above. The only difference is the fact that the method above is considered as a differential approach, which combines both the cash flows and renders the crossover rate as an outcome.
Analysis of Crossover Rate
As discussed earlier, it can be seen that crossover rate is used to determine which of the two projects are desirable from the perspective of the company. In this regard, it is important to consider the fact that the calculation involved in estimating the crossover rate offers a very important insight regarding the performance of different projects, which in return helps to weigh the alternates.
This is because in isolation too, NPV and IRR are widely used metrics when it comes to capital budgeting. There are numerous different implications associated with calculating IRR (and hence, the crossover rate). They are as follows:
- In order to calculate IRR, the same formula is used as the NPV. However, since NPV is substituted as zero, solving the equation for r renders the IRR. It assumes that all the positive cash flows are reinvested in the business.
- It accounts for time value of money. This is because cash flows for all the subsequent years are discounted in order to arrive at their present value. Therefore, cash flow’s economic life is also inculcated which adds credibility to the stated analysis.
- However, IRR does not factor in payback, and the relative size of investment, with relative returns generated. Since crossover rate focuses on the differential, the results derived are not always very accurate.
