Either you are an individual investor, corporate investor, or student of finance, one statement must be agreed upon. Investment is very critical to the long-term profitability of any business.
It gives the security that the profit is continuously growing without any sales efforts or sales growth for corporate investors. For an individual investor, investments are a road to financial independence in the long-term. Investments are a source of financial security and income as well.
Irrespective of investment motives, every investor wants a maximum return for a given level of risk. Besides, they want their investments to be optimized in such a way that they can make the most out of them.
Corporations go for portfolio investments, and their professionals are doing calculations all the time to make an optimized portfolio. At the same time, too many software and Robo-advisors have facilitated individual investors to lower their burdens.
Because understanding the heavy concepts of portfolio diversification, frontier, capital asset lines, optimization of portfolio weights, variance, etc., can be frustrating for them.
However, some basic knowledge of the field you are in is always good. Therefore, we have made this effort to explain different facets of investment. We will discuss risks, returns, portfolio diversification, weights, and optimization of portfolio weights for maximum return.
Risk And Return
The concept of risk and return is the backbone of investment. Any investor’s primary objective, either corporate or individual, is to earn a profit on the investment. So return is the first brick of the building named as an investment.
On the other hand, it is a very famous and proven financial fact that as the return of any investment increases, the associated risk also increases. So, we can say,
Higher is the risk; higher is the return.
The two concepts are highly correlated to each other. Any investor is looking at both aspects simultaneously because he wants a return with security. Every decision made in investments, either it is related to the type of investment, industry, or portfolio weight, the foundation of the decisions is expected return and associated risk.
Therefore, it is important to understand that risk and return are the two most important facets of any investment strategy, portfolio, or investment.
Portfolio And Portfolio Diversification
A portfolio in investment is just a set of different assets an investor has invested in. A portfolio might consist of different financial instruments like bonds, common stocks, cash equivalents, commercial papers, commodities, or cash.
For any portfolio to work in favor of the investor, portfolio diversification is the key. Now, what is portfolio diversification?
It is a process of making an investment in diversely spread asset classes like bonds, stocks, cash, commodities, etc., and financial instruments of different industries like cement, automobiles, space technology, etc.
The purpose of portfolio diversification is to spread the overall risk that an investor might be exposed to in investing all money in one asset class or type.
In other words, portfolio diversification is the process of diversifying an asset’s risk to a minimum level.
To further understand the concept, imagine investing all of your money in oil industry stocks. You will be enjoying higher and continuous returns until stocks perform well, but what if the oil market crashes?
Now you can understand that portfolio diversification will balance off your loss from one asset type with the return of another asset. So, even in the worst scenario, you will be better off than others.
But, a well-diversified portfolio is all about the allocation of portfolio weights. Let’s get to the concept of portfolio weights.
Portfolio Weights
Let’s define the term before breaking it down.
Portfolio weight is the percentage investment of a particular asset in an investment portfolio.
To make it much simple, imagine a pie. If you cut it into eight parts, eight slices will have a certain portion of the pie. If we idealize that each slice is equal, so each slice will be 12.5% of the total pie. Now, this is the weight of each pie.
In investments, the portfolio weight is the value of a certain type of asset in the investment portfolio’s total value.
Portfolio Weights Basis For Portfolio Weights
There can be different ways for calculating the portfolio weights, and each method has a foundation on which the weight for different assets is calculated in an investment portfolio.
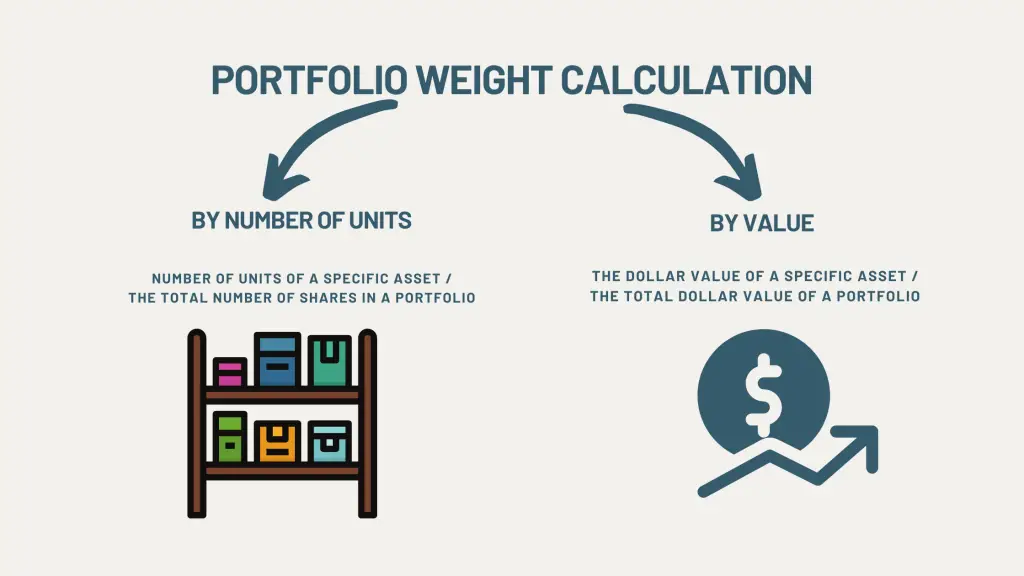
The most common ways are
- By Number Of Units
- By Value
By Number Of Units
For calculation of the portfolio weight in an investment portfolio based on the number of units, you have to simply divide the number of units of a specific asset by the total number of units of all the assets in the portfolio.
For example, a portfolio has 5000 shares of stock A, 2000 shares of stock B, and 1500 shares of stock C. We want to calculate the weight of stock A.
If we add up all the stocks, the total number of shares in a portfolio will be 8500 shares. To find the weight of stock A, we will divide 5000 by 8500.
The answer will be 58.8% means that stock A constitutes 58.8% of the total portfolio as per the number of units.
By Value
Calculating the portfolio weight based on each asset’s value in the portfolio is a more common way than calculating by units. To calculate the portfolio weight by value, the dollar value of the specific asset in a portfolio with the total dollar value of the investment portfolio.
Let’s take another example of a portfolio where stock A values $500; stock B has the value of $800, and stock C also has $800.
What if we want to find the portfolio weight for asset B?
The total value of the portfolio will be the sum of all three stocks that is $2100. We will divide the value of stock B by the total value of the portfolio.
The answer will be 38% means that the value of stock B is 38% of the total value of the portfolio.
The Number Of Units Vs. Value; Which Strategy Is More Complaint?
We have discussed two approaches for calculating the portfolio weights, but the question remains: Which basis is more realistic and translates the true information?
Either method can be used and legitimate, but the calculation of weights by the total portfolio value is a more realistic approach. It will give you a real picture of what you are looking for. For instance, your investment goal was that no single type of asset should exceed 20% value of the total portfolio.
You may have invested in a blue-chip company with high share prices but fewer shares in this scenario. If you use the unit basis, you might find out that the asset value is less than 20% of the total portfolio.
However, it is quite possible that the value of those few stocks might exceed the 20% goal.
Therefore, the value method is more reliable, and it also depends on the investment goals.
Optimization Of Portfolio Weights
We talked about return, risk, portfolio diversification, weights, maximum return, and minimum risk. But, how is this all possible?
A well-diversified portfolio is a roadmap to your goal of maximum returns for a given level of risk tolerance. But how a well-diversified portfolio is created? A lot of research, knowledge, and foresight is required for this.
The process of diversification is standing on the foundation of optimizing portfolio weights. Let’s look at what optimization of portfolio weights is?
Portfolio optimization creates a balanced portfolio by spreading the investment across different types of assets. It is regarded as a risk mitigation strategy.
Let’s look at how optimization of each portfolio weight is important for risk mitigation.
Weight Optimization
Every investor has different investment motives, risk tolerance, and return expectations. Therefore, the optimum portfolio weight for each investor varies.
We can say that this is the point where your investing intelligence and foresightedness intervenes. Based on your assessment, you will decide what weight to assign to a specific asset class.
For instance, in the broadest scenario, we can say that 40% of the investment will be in blue-chip stocks, 20% in growth-stocks, and 40% in bonds. This combination might be optimum for my risk and return preferences but not for yours.
You got the point, right?
Let’s try to resolve it by the example of how to calculate the optimum weight.
Sally is an investor who has a risk tolerance of 25%. She has decided to invest in 3 different asset classes. The three classes are bonds, blue-chip stocks, and growth stocks.
Let’s give imaginary names.
Bond XYZ: 10% risk(least riskier option)
Stock ABC: 30%
Stock LMN: 45%
Now, we have to find what an optimum weight for each class should be.
The equation of portfolio will be something like
(weight of bonds) + (weight of stock ABC) + (weight of stock LMN) =1(Total portfolio)
If we talk about the risk of the portfolio, the equation should be
0.1(weight of bonds) + 0.3(weight of stock ABC) + 0.45( weight of stock LMN) =0.15(risk tolerance)
You can see that this formula is unsolvable because there are too many variables. Here will be the test of the personal assessment of an investor.
Let’s discuss this scenario for a risk-averse person.
He decides to invest 10% in the riskier stock LMN. Now, if we substitute it in the equation, we know that bonds XYZ and stock ABC constitute 90% of the portfolio.
Weight of Bonds XYZ+ Weight of Stocks ABC= 0.9
Weight of Bonds XYZ = 0.9 – Weight of Stocks ABC
Let’s put the weight of bonds XYZ in above equation of risk.
0.1(0.9 – Weight of Stocks ABC) + 0.3(weight of stock ABC) + 0.45( 0.1) =0.25(risk tolerance)
0.2(weight of stock ABC) + 0.09 = 0.015
weight of stock ABC= 0.115/0.2
Weight of Stock ABC= 0.575
Now, if we put the value in the equation, we can find the value of portfolio weight for bonds.
Weight of Bonds XYZ = 0.9 – 0.575
Weight of Bonds XYZ = 0.325%
Final Words
We have tried to comprehensively cover the topic of portfolio weights, and we hope that it will contribute to your understanding of investments, portfolio diversification, risk, and return.
