Probability refers to the chances of an event happening in statistical terms. The probability of two events means the chances of both events happening at the same time, one at a time, or one after the other.
The rule of addition describes the relationship between the probability of two events when they can be mutually exclusive or mutually non-exclusive to each other.
Addition Rule of Probabilities – Definition
The addition rule of probabilities is used to compute the probability of two events happening at the same time when they are mutually exclusive or non-exclusive.
It combines the probability of two mutually exclusive events happening and then the probability of either of the two events happening when they are mutually non-exclusive.
Probability is a statistical term describing the likelihood of an event happening. In simple words, it is the percentage chance of an event happening out of 100%.
When two events are mutually exclusive, then the probability of two happening at the same time is zero. Therefore, it’s easier to apply the addition rule in such scenarios.
How Does it Work?
Let us first understand a few key concepts in the addition rule of probabilities.
A set of probabilities is taken out of the set of sample spaces for all events. A sample space includes all possible scenarios under the given conditions.
Two mutually exclusive events mean if one happens then the second one does not happen. It means the chances of both events happening at the same time are zero.
Mutually non-exclusive events mean one of two or both can happen at the same time. It means the chances of both events taking place at the same time are probable.
Independent events can happen without affecting each other. Setting a sample space for independent events is often a challenging task as the probability of events can be unlimited.
Once these parameters are set, we can then use the formula listed below to calculate the probability of events.
How to Calculate Probabilities with the Addition Rule?
The addition rule combines two probabilities into one with the following formula:
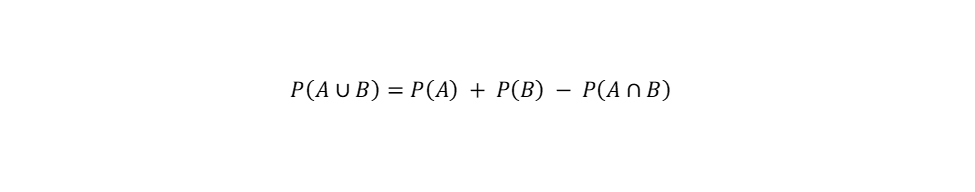
It can also be written as:
P (A or B) = P(A) + P(B) – P (A and B)
When both events A and B are mutually exclusive, then P (A and B) =0. Therefore,
P (A or B) = P(A) + P(B)
We can use the simple step-by-step guide to use the addition rule of probability.
The first step is to calculate the probability of events A and B separately.
The second step is to calculate the probability of (A and B) when they are mutually non-exclusive.
The third step is to use the formula and calculate the probability of (A or B).
The probability of (A and B) is calculated by multiplying the P(A) with P(B).
Mutually exclusive events are not independent of each other as they depend on each other to some extent.
It is because both these events belong to the same sample size and P(AB) can only be zero when they are both independent.
Addition Rule of Probability – Mutually Exclusive Events
Two mutually exclusive events cannot happen simultaneously but must not be independent of each other.
For example, if you flip a coin, the probability of either Heads or Tails is 50% for each. Both cannot happen simultaneously, but one will happen if the other does not.
So, these are mutually exclusive and non-independent of each other.
Further, the two events become independent when considered over a sequence or series. For example, if we flip the coin and get Heads, it does not guarantee that the next flip will produce Tails to complete the 100% probability of two events.
Therefore, the sample scale of the events decides the outcome or probabilities of the events as well.
Addition Rule of Probability – Mutually Non-Exclusive Events
The mutually non-exclusive events mean both events can happen at the same time. Therefore, the probability of P(AB) is not equal to zero.
For example, if there are 30 students in a class with 15 boys and girls. The chances of a boy and a girl getting 90% marks in a subject are mutually non-exclusive events.
In this case,
P (A or B) = P(A) + P(B) – P (A and B)
The addition rule only concerns one event happening at the same time, we must then deduct P (A and B) from the total of both probabilities of these events.
Examples
Let us now consider some examples of the addition rule of probabilities under different scenarios.
For example, in a class with 30 students. There are 15 boys and girls each in the class. In the previous term exam, 5 boys and 4 girls achieved grade A.
We need to calculate the probability of a boy or any student getting a Grade A again in the coming exams.
Solution:
Let’s suppose P(A) is the probability of grade A for any student and P(B) is the probability of a boy being chosen.
There are 9 grade A students out of 30. Therefore, P(A)=9/30.
There are 15 out of 30 students are boys. Therefore, P(B)=15/30.
Since 5 boys previously received Grade A, therefore:
P (A and B) = 5/30
Now we can use the addition rule to calculate the probability of either event:
P (A or B) = P (A) + P(B) – P (A and B)
P (A or B) = 9/30 + 15/30 – 5/30
P (A or B) = 9 + 15 – 5/30= 19/30
P (A or B) = 0.63 or 63%
Example 2
A company surveyed 100 people to know their preferred social media (SM) sites. The results of the survey are displayed in the table below.
| Preferred SM | Male | Female | Total |
| 18 | 28 | 46 | |
| 23 | 11 | 34 | |
| Other | 13 | 7 | 20 |
| Total | 54 | 46 | 100 |
Let us find the probability of a random male preferring Facebook.
A total of 46 people liked Facebook. Therefore:
P (Prefer Facebook) = 46/100 or 0.46
Similarly,
P (Prefer Twitter) = 34/100 = 0.34
If we want to know the probability of a female preferring Facebook, then:
P (Female Prefer Facebook) = 28/100
The probability through the Rule of addition for both conditions can be written as:
Probability (Female or Prefer Facebook) = 28/100 + 46/100 – 11/100
Probability (Female or Prefer Facebook) = 63/100 or 0.63
